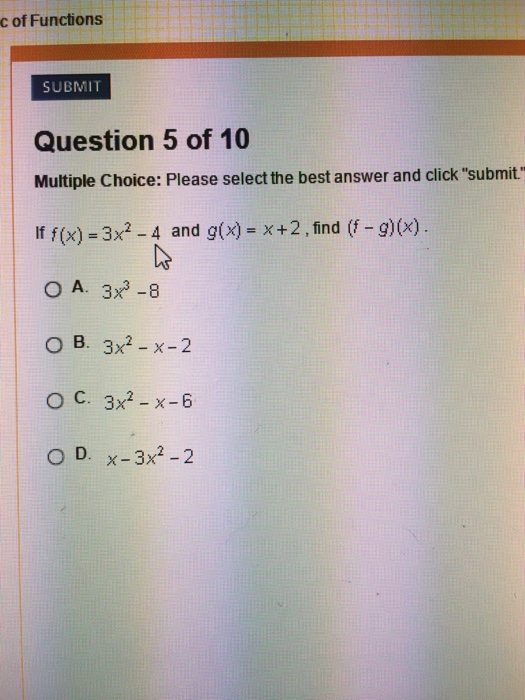
Find (s p)(x) for f and g below s(x) = 4x2 8x 8 (29) p(x) = x 4 (30) Find (g f q)(t) for g, f, and q below q(t) = p x (31) f(t) = x2 (32) g(t) = 5x9 (33) Find (f g h j)(x) for the functions below HINT Look at f and think about what will happen to it no matter what we plug into f j(x) = 4x9 3sin(x) (34) h(x) = ln(x) (35) g(x) = 4x (36F (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f (x2) = 3(x2)−4 f ( x 2) = 3 ( x 2) 4 Simplify each term Tap for more steps Apply the distributive property f ( x 2) = 3 x 3 ⋅ 2 − 4 f ( x 2) = 3 x 3 ⋅ 2 4 Multiply 3 3 by 2 2 f ( x 2) = 3 x 6 − 4 f ( x 2In this video we learn about function composition Composite functions are combinations of more than one function In this video we learn about f(g(x)) and g
Suppose F X X 2 What Is The Graph Of G X F 3x
F(x)=x^2 g(x)=2x+1
F(x)=x^2 g(x)=2x+1-Find f(g(x)) f(x)=1/(x2) g(x)=4/x Set up the composite result function Evaluate by substituting in the value of into Simplify the denominator Tap for more steps Factor out of Tap for more steps Factor out of Factor out of Factor out of To write as a fraction with a common denominator, multiply by 518 views around the world You can reuse this answer Creative Commons License




Warm Up Let F X Write The Equation For G X In Terms Of X 1 G X 3 F X 2 G X F 1 3x 3 G X F X 3 Ppt Download
G(f (x)) g ( f ( x)) Evaluate g(f (x)) g ( f ( x)) by substituting in the value of f f into g g g(x−2) = (x−2)2 g ( x 2) = ( x 2) 2 Combine the opposite terms in (x− 2)2 ( x 2) 2 Tap for more steps Add − 2 2 and 2 2 g ( x − 2) = x 0 g ( x 2) = x 0 Add x x and 0 0 g ( x − 2) = x g ( xSPM Add Math Form 4 FunctionThis short video is going to guide you how to find the f(x) using the substitution method Hope you find this method helpfuI'll give you a hint to get you started If
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe Chain Rule says the derivative of f (g (x)) = f' (g (x))g' (x) The individual derivatives are f' (g) = cos (g) g' (x) = 2x So d dx sin (x 2) = cos (g (x)) (2x) = 2x cos (x 2) Another way of writing the Chain Rule is dy dx = dy du du dxThere is no particular method that works for any combination of mathf(x) \cdot g(x)/math but your integral in particular is of the form math\int e^u du=e^uc/math We can then solve by letting mathu=02x/math and we can differentiate t
2*f (x) means two multiplied by the function f f (2x) means the function at 2x; Example 16 Let f(x) = x2and g(x) = 2x 1 be two real functions Find (f g) (x), (f – g) (x), (fg) (x), ("f" /𝑔) (x) f(x) = x2 & g(x) = 2x 1 (f g) (x) = fG(x) = 2x 1 g ( x) = 2 x 1 Set up the composite result function f (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f (2x1) = (2x1)2 − 4 f ( 2 x 1) = ( 2 x 1) 2 4 Simplify each term Tap for more steps Rewrite ( 2 x 1) 2 ( 2 x 1) 2 as ( 2 x




If F X 2 X 3 G X X 3 X 4 And H X 2 2x 1 X 2 X 12 Then Find Lim Xrarr3 F X G X H X




If F X X 2 And G X 2x Then Evaluate I F G 3 Ii F G 2 Iii F G 1 Iv F G 5
F (x) = x2 − 4 f ( x) = x 2 4 ;Inverse Functions Inverse functions are functions that undo one another In other words, if f1 (x) is the inverse of f(x), then f(f1 (x)) = f1 (f(x)) = xWe can use this definition to solveOr the value of the function evaluated at 2x Giving a name f to a function for the function using independant variable x will be named as f (x), to be read, "the function f of x" Shown alone, f and x are not factors, but are a complete name




F X X 2 What Is G X Brainly Com




F X X 2 What Is G X Brainly Com
It is possible that the midpoint and/orTo find the answers, I can either work symbolically (like in the previous example) and then evaluate, or else I can find the values of the functions at x = 2 and then work from there It's probably simpler in this case to evaluate first, so f (2) = 2 (2) = 4 g (2) = (2) 4 = 6 h (2) = 5 – (2) 3 = 5 – 8 = –3Completing the square, f(x)=\frac{3}{4}(\frac{1}{x}\frac{1}{2})^2, so x=2 is a global minimum, and there is no minimum, absolute or relative, for x\gt 1 Completing the square, f ( x ) = 4 3 ( x 1 2 1 ) 2 , so x = − 2 is a global minimum, and there is no minimum, absolute or relative, for x > − 1




F X X 2 What Is G X Brainly Com
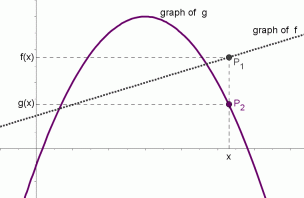



Graphical Interpretation Of Sentences Like F X G X And F X G X
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! In this composition the independent variable is f(x) because this function is the input The composition is the same as the following (g @f)(x)=g(f(x))=g(x^2)=x^22See first you have to calculate g(1) which is g(1) = (1)^2 2 g(1) = 1–2 = 1 g(1) = f(g(1)) = f(1) Now we will calculate required value of f(g(1)) f(g



Math Scene Equations Iii Lesson 3 Quadratic Equations




F X X 2 What Is G X Brainly Com
As an example, a classic result of Ritt shows that permutable polynomials are, up to a linear homeomorphism, either both powers of x, both iterates of the same polynomial, or both Chebychev polynomials We say f and g commute (with respect to composition) The property is called "commutativity"SOLUTION Find (fg) (x), (fg) (x), (f*g) (x) and (f/g) (x) for each f (x) and g (x) 2 f (x)= 8x^2 g (x)=1/x^2 I'm having trouble understanding what i have to do, please help You can put this solution on YOUR website!Let f_1(x)=x^2 Then f_1'(x)=2x




Area Between F X Sqrt 16 X 2 And G X E X 2 2 Mathematics Stack Exchange
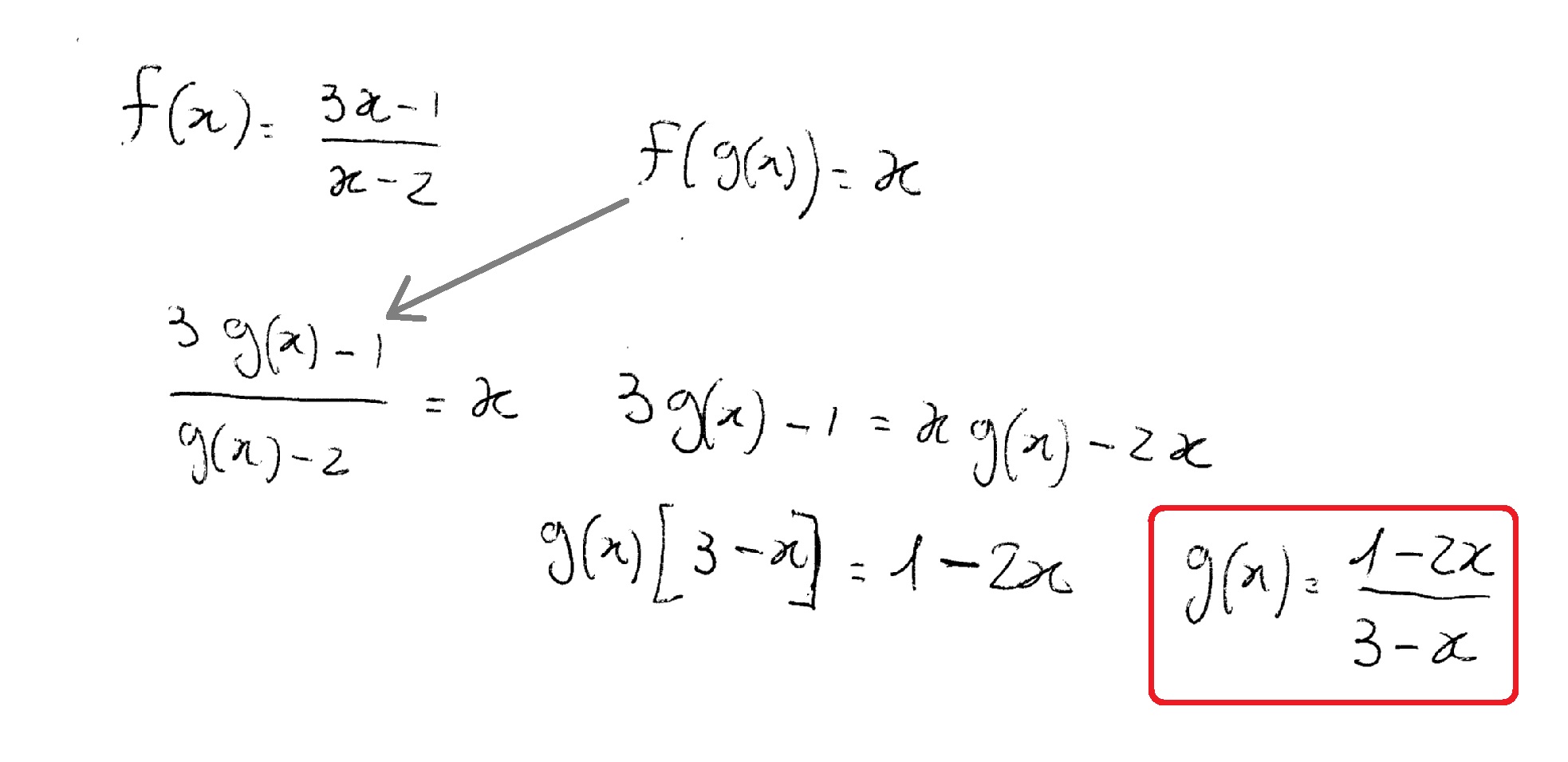



Let F X 3x 1 X 2 And F G X X How Do You Find G X Socratic
Composite Function A composite function is a function which is made by combining two or more than two functions For example, if {eq}f(x) {/eq} and {eq}g(xFind the domain of the composite function f of gIn this math video lesson I review how to graph the exponential equation y=2^x by making a table The table helps when graphing these types of equations #e




F X X 2 What Is G X Brainly Com




F X X 2 What Is G X Brainly Com
G(x) → "g of x" → "operation(s), g, applied to a given quantity or value , x" "g(x) = x1" tells you to simply subtract 1 from whatever xvalue is given g(5)= 5–1=4 g(6)= 6–1=5 g(9)= 9–1=8 g(x)=x1 f(x) → "f of x" → "operations, f, applied to a g #2 the letter which you use to label a function has no special meaning g (x) just identifies a function of x, in the same way as that f (x) does Using a "g" instead of an "f" only means the function has a different label assigned to it Typically this is done where you have already got an f (x), so creating another one would be f(x)*g(x) = (tan(x) 2/x)(x² 8) Apply FOIL in multiplying binomials Multiply the First terms, next is the Outer terms, then the Inner terms, and lastly, the Last terms = tan(x³) 8 tan(x) 2x²/x 2(8)/x Simplifying we get = tan(x³) 8 tan(x) 2x 16/x Now Multiplying it by x to remove the variable in the denominator and we get




7 If F X And G X X2 2x Find Fg X And Its Chegg Com




Find Fog And Gof If F X Sinx G X X 2 Youtube
Free functions composition calculator solve functions compositions stepbystepY = f(x) = x^2 means the independent variable in the equation is x y = f(a) = a^2 means the independent variable in the equation is a the rules are the same the only difference is the variable that the equation is working with that is why when you say f(x) = x^2, f(x) becomes the dependent variable and x is the independent variableWhen you find (f o g)(x), there are two things that must be satisfied x must be in the domain of g, which means x is a real number (pretty easy to do) g(x) must be in the domain of f, which means that 1x 2 ^2 ≥ 4 (when you try to solve this, you get the empty set);




Algebra 2 How To Evaluate A Composition F X G X Youtube




Composite Functions Video Lessons Examples And Solutions
When you combine the two domains to see what they have in common, you find the intersection of everything and nothing is\displaystyle{x}\in\mathbb{R},{x}\ne{1},{2} Explanation \displaystyle{f{{\left({x}\right)}}}\ \text{ is defined for all values of x except values whichAnd "( f o g)(x)" means "f (g(x))" That is, you plug something in for x, then you plug that value into g, simplify, and then plug the result into f The process here is just like what we saw on the previous page, except that now we will be using formulas to find values, rather than just reading the values from lists of points Given f(x) = 2x



Math Scene Equations Iii Lesson 3 Quadratic Equations




Misc 15 Let F X X2 X G X 2 X 1 2 1 Are F G
G ( x ) = \frac { 4 x ^ { 2 } } { x ^ { 2 } 9 } G ( x) = x 2 − 9 4 x 2 For any two differentiable functions, the derivative of the quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the denominator squaredThe composite functions of higher math often use h(x) and g(x), in combination,,defining which comes first, and which is second The substitution is bad enough, but using y's would make it worse In summary, feel free to immediately use "y =" instead of "h(x)", if it clarified the problemLearn how to solve f(g(x)) by replacing the x found in the outside function f(x) by g(x)




Let F X X Cos X 2 And G X Be The Inverse Function Of F X Then G 3 Equals To Youtube




Verifying Inverse Functions By Composition Not Inverse Video Khan Academy
given f(x)=x^26x8 and g(x)=x2 solve f(x)=g(x) using a table of values Guest 0 users composing answers The functions are combined to form the new functions h(x) = f(x) g(x) and j(x) = f(x) g(x) Point (6, 2) is in the function h(x), while the point (2, 10) is in the function Simpson's rule Is the simpson's rule always more accurate than the midpoint rule and trapezoidal rule? 1 Answer AJ Speller (f ∘ g)(x) = f (g(x)) = f (x 2) = (x 2)2 Click on the link below to see another example If f (x) = x2 and g(x) = x 2, what is (g ∘ f)(x)?




Warm Up Let F X Write The Equation For G X In Terms Of X 1 G X 3 F X 2 G X F 1 3x 3 G X F X 3 Ppt Download




Suppose That We Have Two Functions F X And G X Chegg Com
Graph g(x)=x2 Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form The slope of the line is the value of , and the yintercept is the value ofTherefore, let f(x) = g(x) = 2x 1 Then, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg(f⋅g) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f(x) = 0 to also be undefined so that it follows the rules of aF (g (2)), g (x)=2x1, f (x)=x^2 \square!



Math Scene Equations Iii Lesson 3 Quadratic Equations




F X X2 What Is G X 1 16 Brainly Com




F X 2x 3 5x 2 G X 2x 1 Find F G X Youtube




If F X 3x 2 And G X X 2 Then Fog X Youtube




F X X2 What Is G X Brainly Com



Markwaltermath Weebly Com Uploads 2 2 1 9 Winter Break Part 2 Pdf




Calculus Practicals Maxima And Minima Derivative




Find A F G B F G C Fg And D F G And Chegg Com




F X X 2 What Is G X Brainly Com
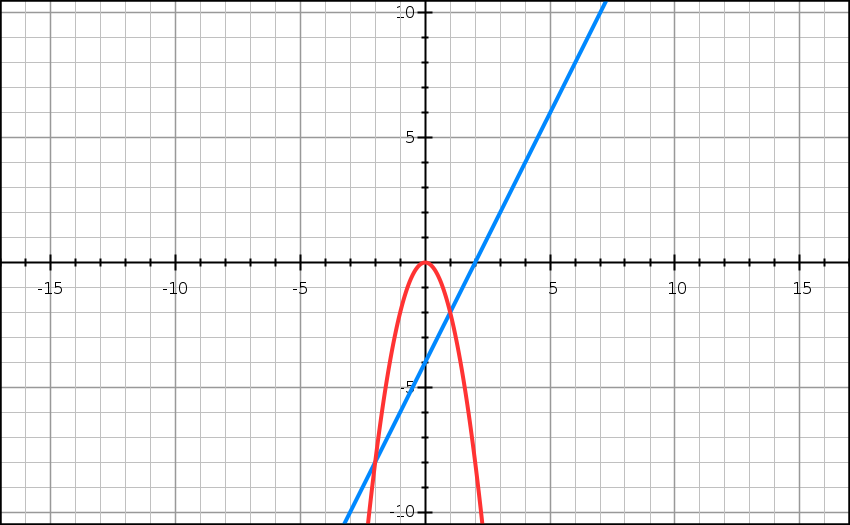



How Do You Draw F X 2x 2 And G X 2x 4 On The Same Graphs Socratic




F X X 2 What Is G X Brainly Com




Answered The Functions F G And H Are Defined Bartleby




Given That F X 2 X 4 And G X 3 X 5 Find Gf 3 With Noob Like Steps Please I Need A Really Clear Working To Fully Understand Thanks 3 Socratic




F X X2 What Is G X Brainly Com




If F X X 2 2 And G X 2x 2 X 3 Find F G X Brainly Com




Finding Composite Functions Video Khan Academy




Let F X X 2 And G X 2x 1 Be Two Real Functions Find F G X F G X Fg Youtube



Manipulating Graphs
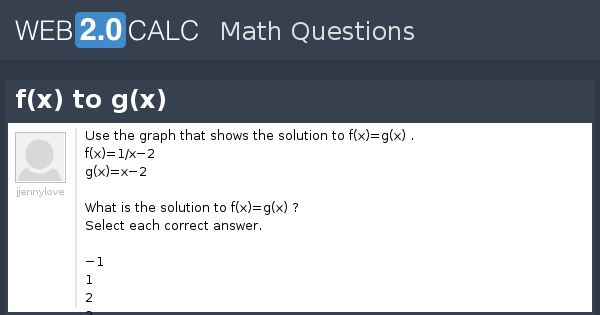



View Question F X To G X




F X X2 What Is G X Brainly Com




How To Evaluate Composite Functions Video Lesson Transcript Study Com




If F X 2x And G X X 2 2 1 Then Which Of The Following Can Be Discontinuous Function Youtube




Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G




Please Help Suppose F X X 2 What Is The Graph Of G X 1 4 F X Brainly Com




How To Find The Derivative Function Of G X 3 X 2 F X F X H F X H Socratic




Composite Functions
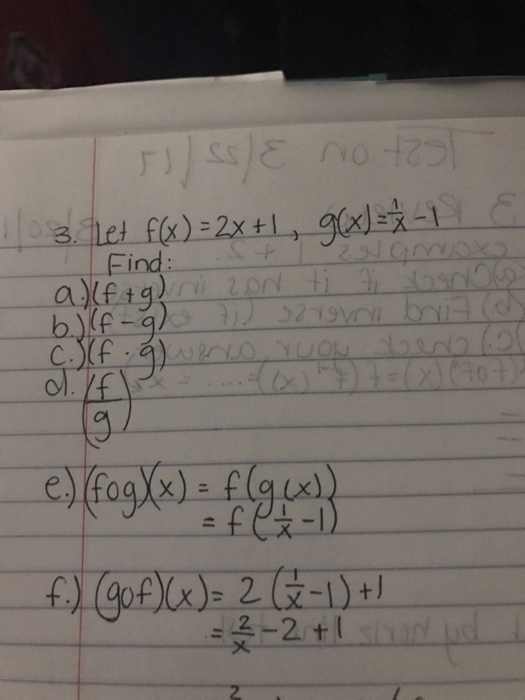



Let F X 2x 1 G X 1 X 1 Find A F G Chegg Com



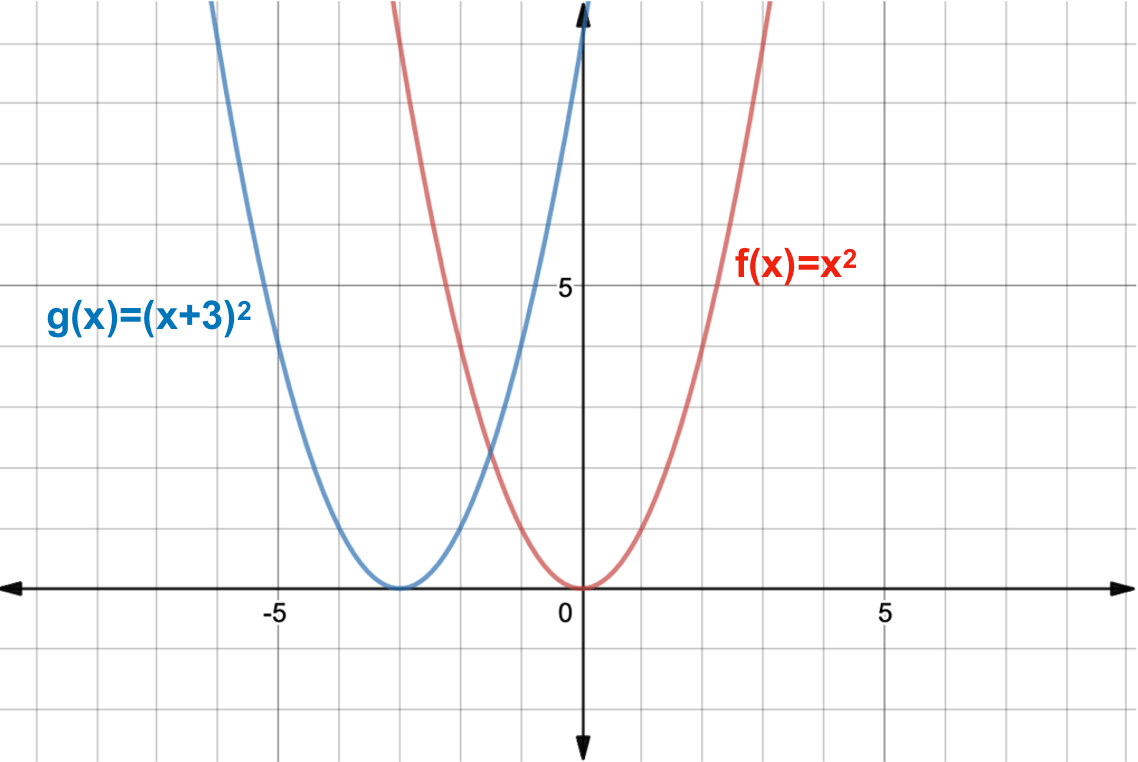
Solution The Function F X X2 The Graph Of G X Is F X Translated To The Left 6 Units And Down 5 Units What Is The Function Rule For G X




Q If F X X2 6x A G X X2 4x B H X X2 14x C And Youtube
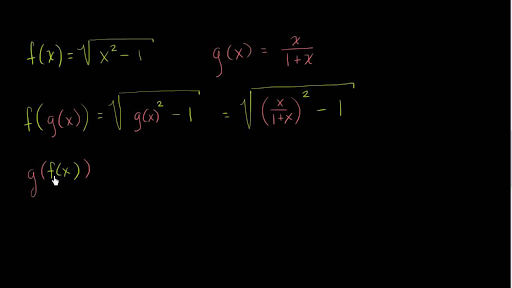



Finding Composite Functions Video Khan Academy



F X X 2 What Is G X Apex




Chapter 2 Problems




F X X 2 What Is G X Brainly Com




Key Concept 1 Example 1 Operations With Functions A Given F X X 2 2x G X 3x 4 And H X 2x 2 1 Find The Function And Domain For Ppt Download




Find The Greatest Common Divisor Of F X 2x 3 2x 2 X 4 And G X X 4 3x 3 4x 2 3x Mathematics Stack Exchange



What Is A Function Transformation Expii




Please Help F X X 2 What Is G X Brainly Com




If F G X 4x2 8x And F X X2 4 Then G X A 4 Maths Relations And Functions Meritnation Com




F X X 2 What Is G X Brainly Com



Solving Equations Graphically




Quantitative Aptitude Algebra Functions Let F X X 2 And G X 2 X Handa Ka Funda Online Coaching For Cat And Banking Exams
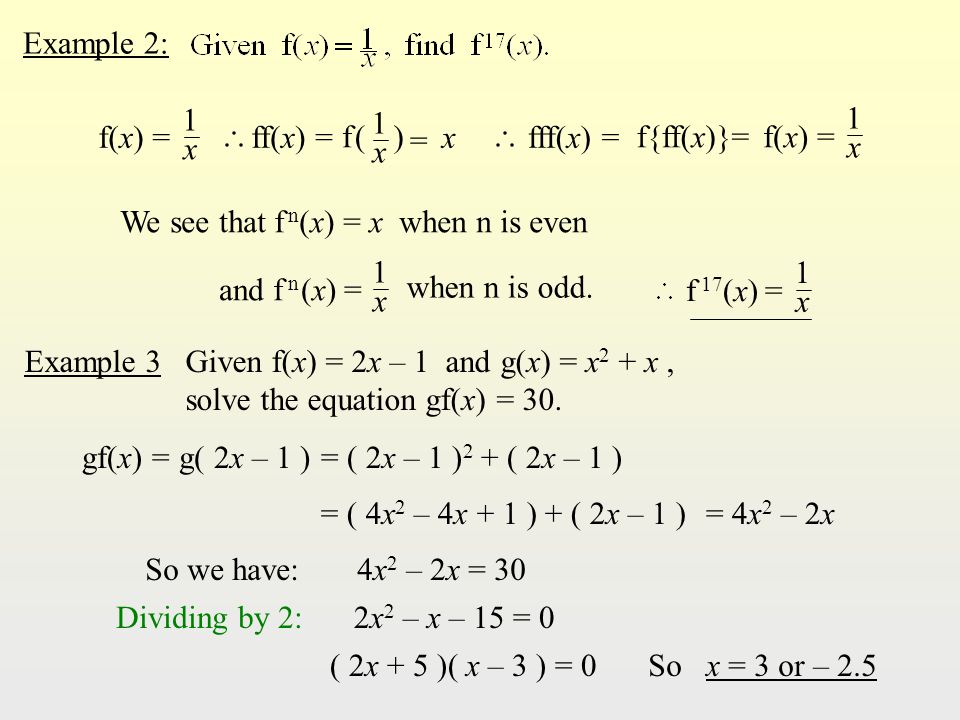



Composite Functions The Composite Function Fg Means Apply The Rule For G Then Apply The Rule For F So If F X X 2 And G X 3x 1 Then Fg 2 Ppt Download




F X X 2 What Is G X Brainly Com



If F X 3x 2 4 And G X X 2 Find F G X Chegg Com



Suppose F X X 2 What Is The Graph Of G X F 3x
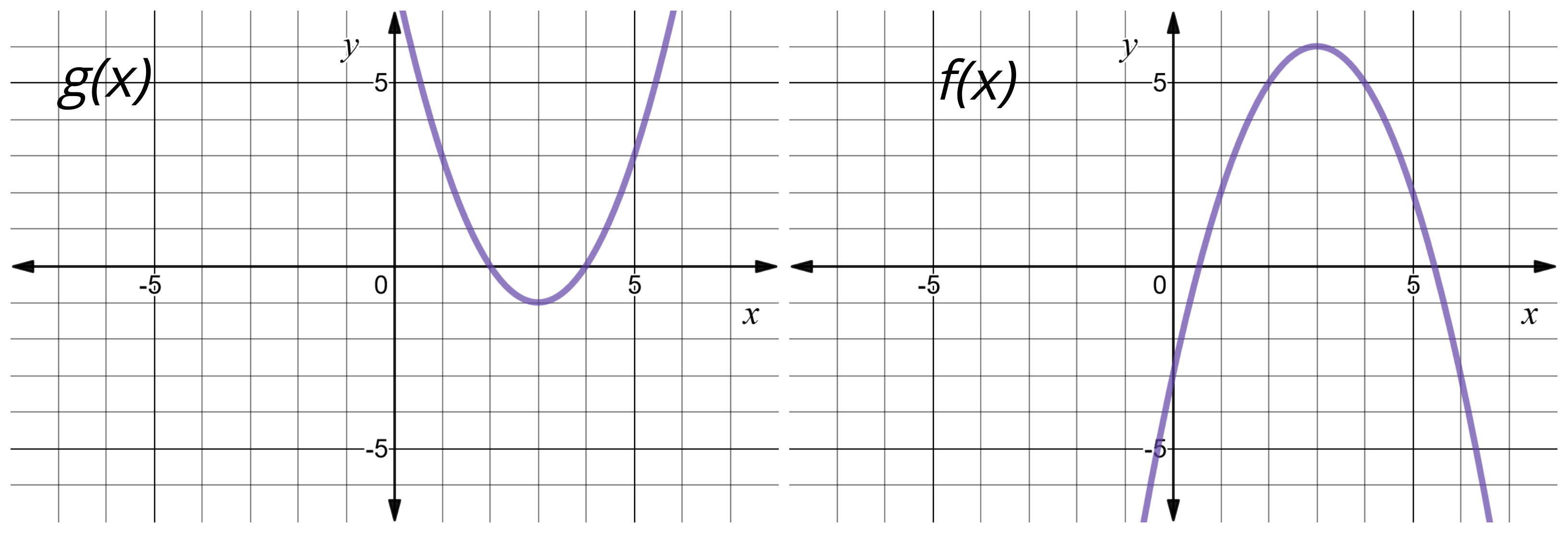



Composing Functions At A Point Expii




F X X 2 What Is G X Brainly Com
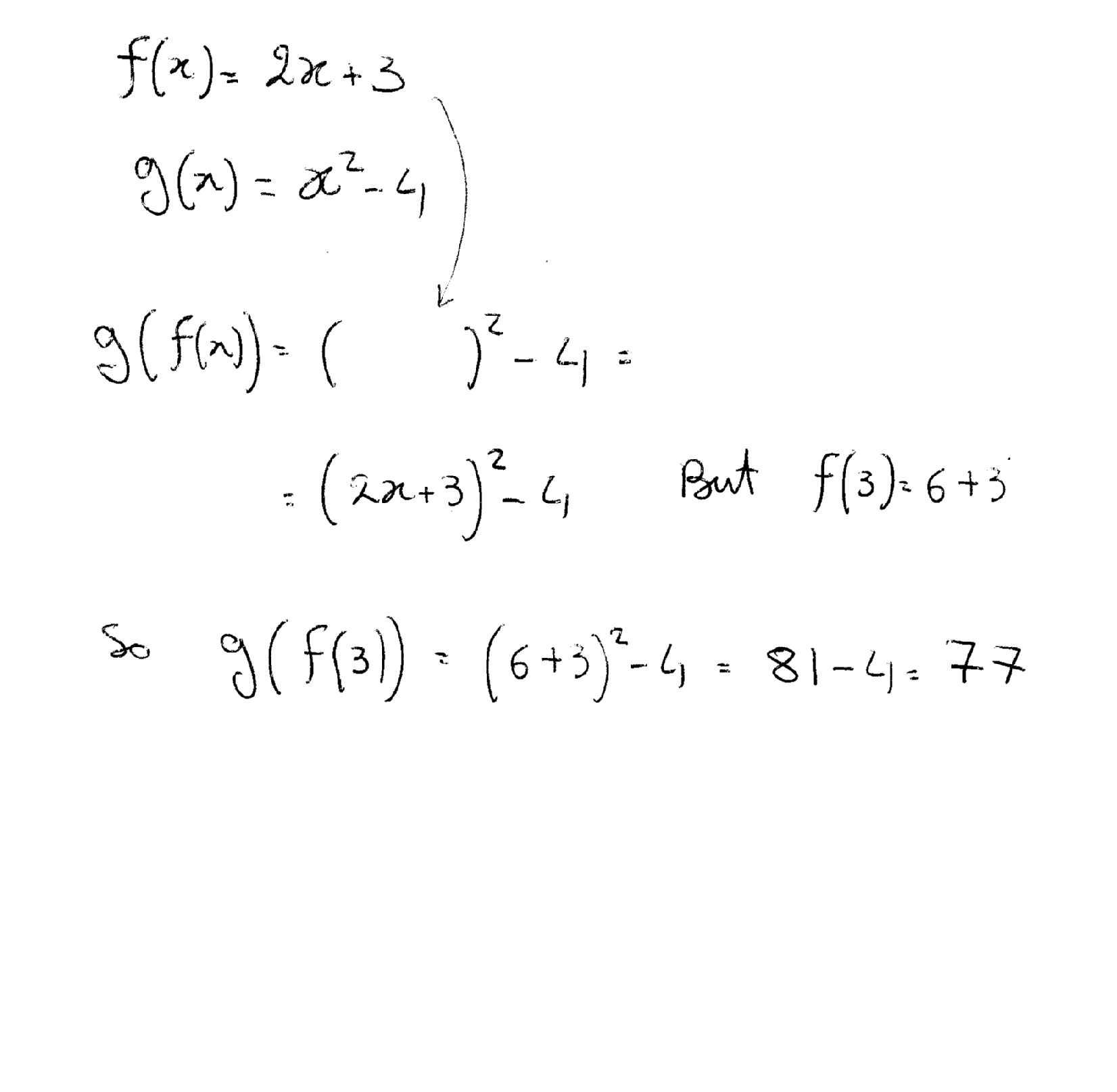



Let F X 2x 3 And G X X 2 4 And H X X 3 2 How Do You Find G F 3 Socratic



Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Preap alg ii 6 3 Pdf



How Do You Find The Area Between F X X 2 2x 1 G X 3x 3 Socratic
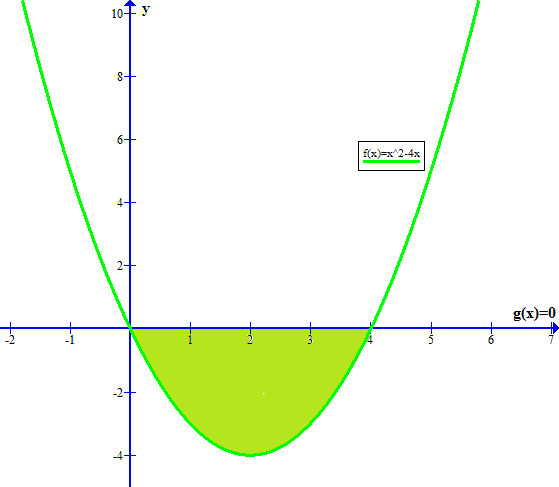



How Do You Find The Area Between F X X 2 4x G X 0 Socratic




F X And G X Ssdd Problems
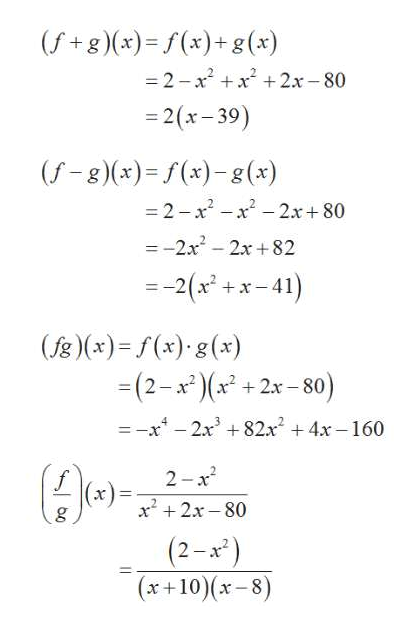



Answered For The Functions F X 2 X2 And G X X2 Bartleby




Answered Consider The Following Functions F X Bartleby
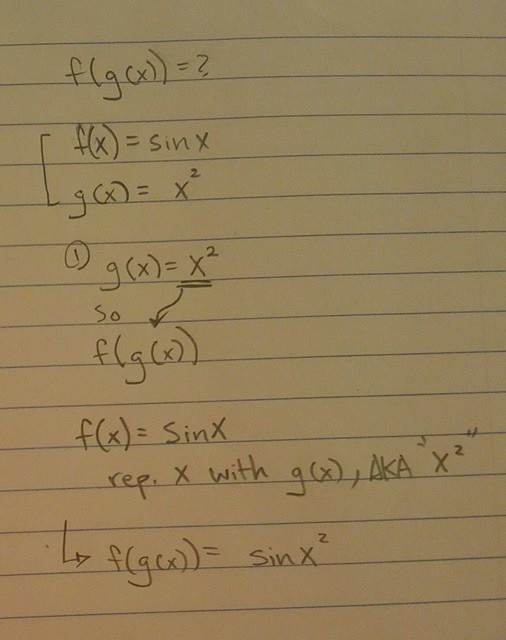



What Is The Continuity Of The Composite Function F G X Given F X Sinx And G X X 2 Socratic
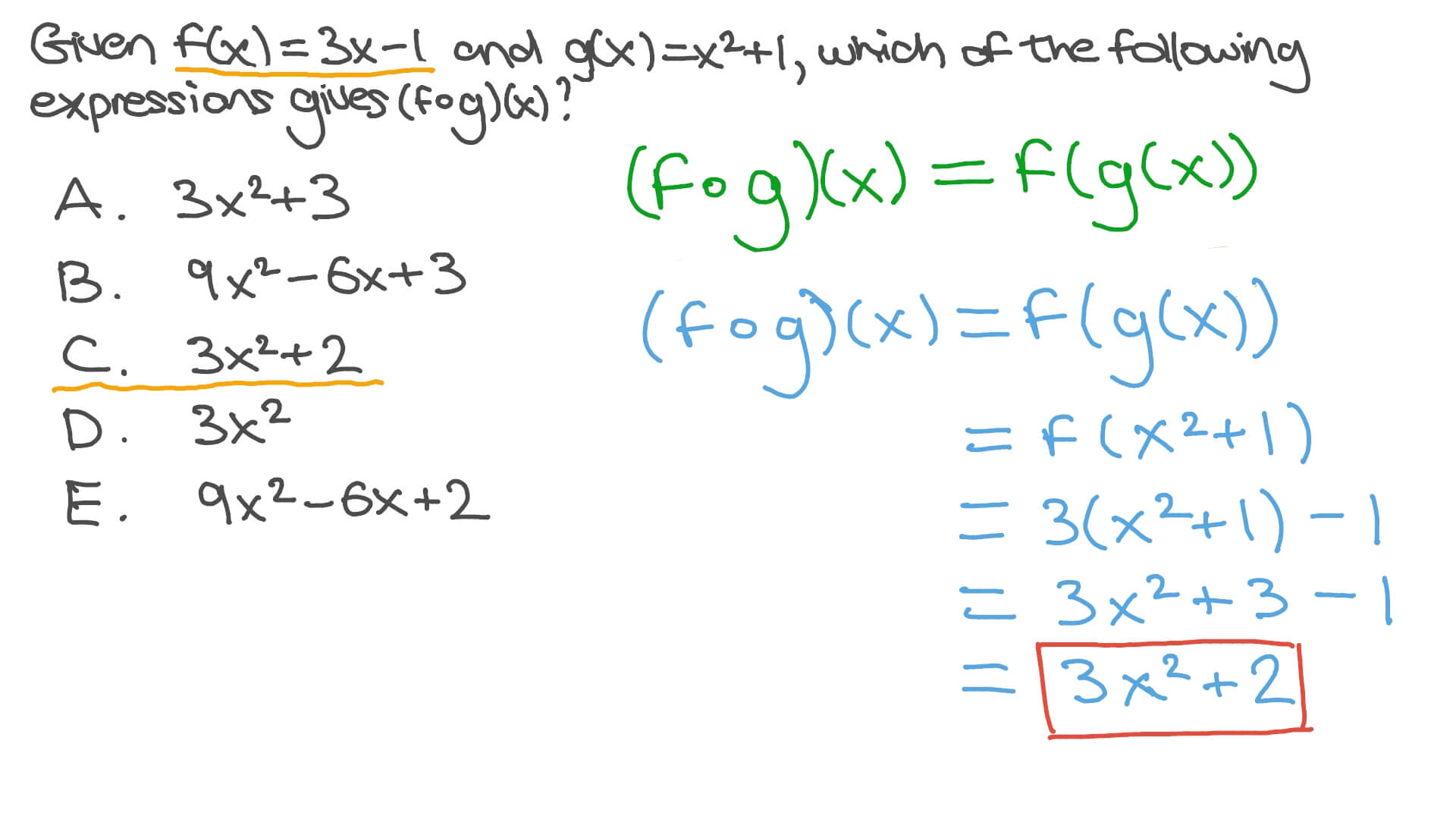



Question Video Finding The Composite Of Two Functions Nagwa




F X X 2 What Is G X Brainly Com
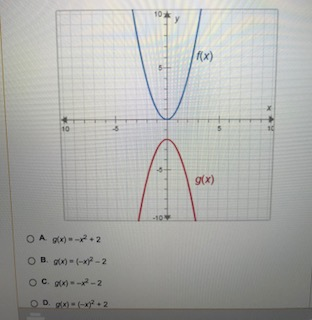



The Functions F X And G X Are Shown On The Graph Chegg Com




Function Composition Given F X 2x 2 And G X 2 Find F ºg X F ºg X F G X Start On The Inside F G X G X 2 So Replace It F G X F 2 Ppt



Suppose F X X 2 What Is The Graph Of G X F 4x




F X X 2 What Is G X Brainly Com



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf




F X X2 What Is G X F X G X 2 2 15 Brainly Com



Suppose F X X 2 What Is The Graph Of G X 1 3f X




F X X 2 What Is G X Brainly Com




F X X 2 What Is G X A G X X 2 4 B G X X 2 4 C G X 4x 2 D G X X 2 4 Brainly Com
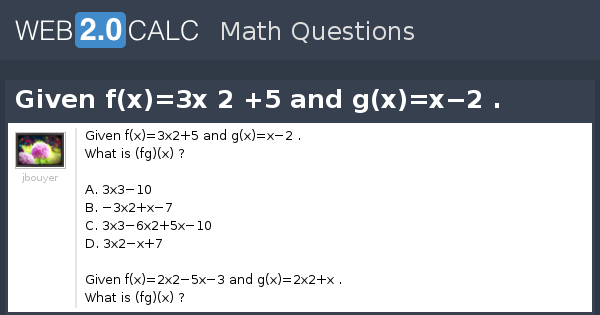



View Question Given F X 3x 2 5 And G X X 2




F X X 2 What Is G X Brainly Com



Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant



Solution If F X 2x 1 And G X X 2 Find 1 G G X 2 G F X 3 F G X 4 F F X
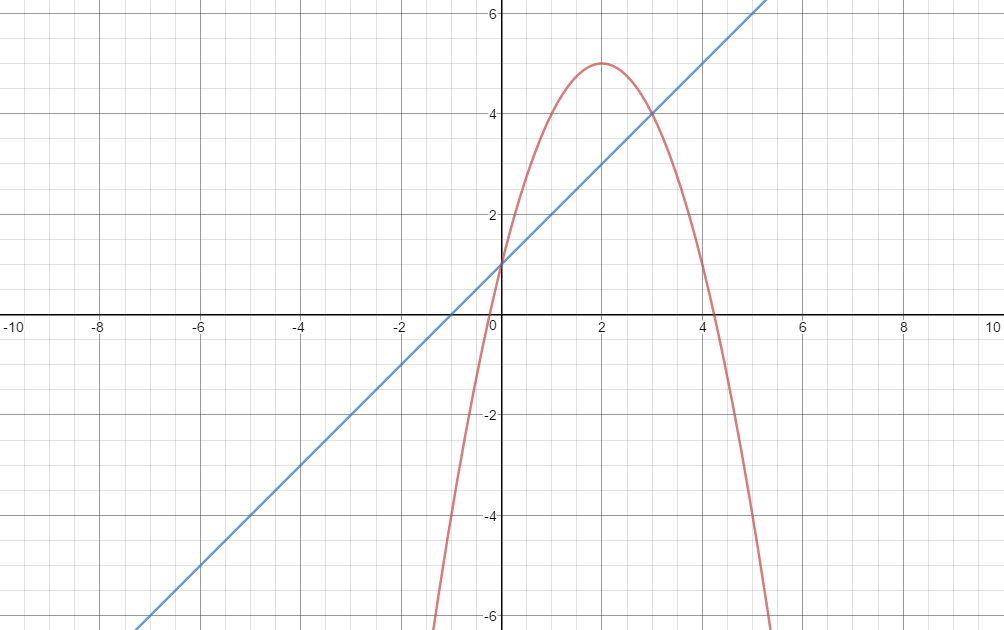



How Do You Find The Area Between F X X 2 4x 1 G X X 1 Socratic




F X X2 What Is G X Brainly Com




Given F X X2 2x And G X 6 X2 Find F G F G Fg And F G Youtube
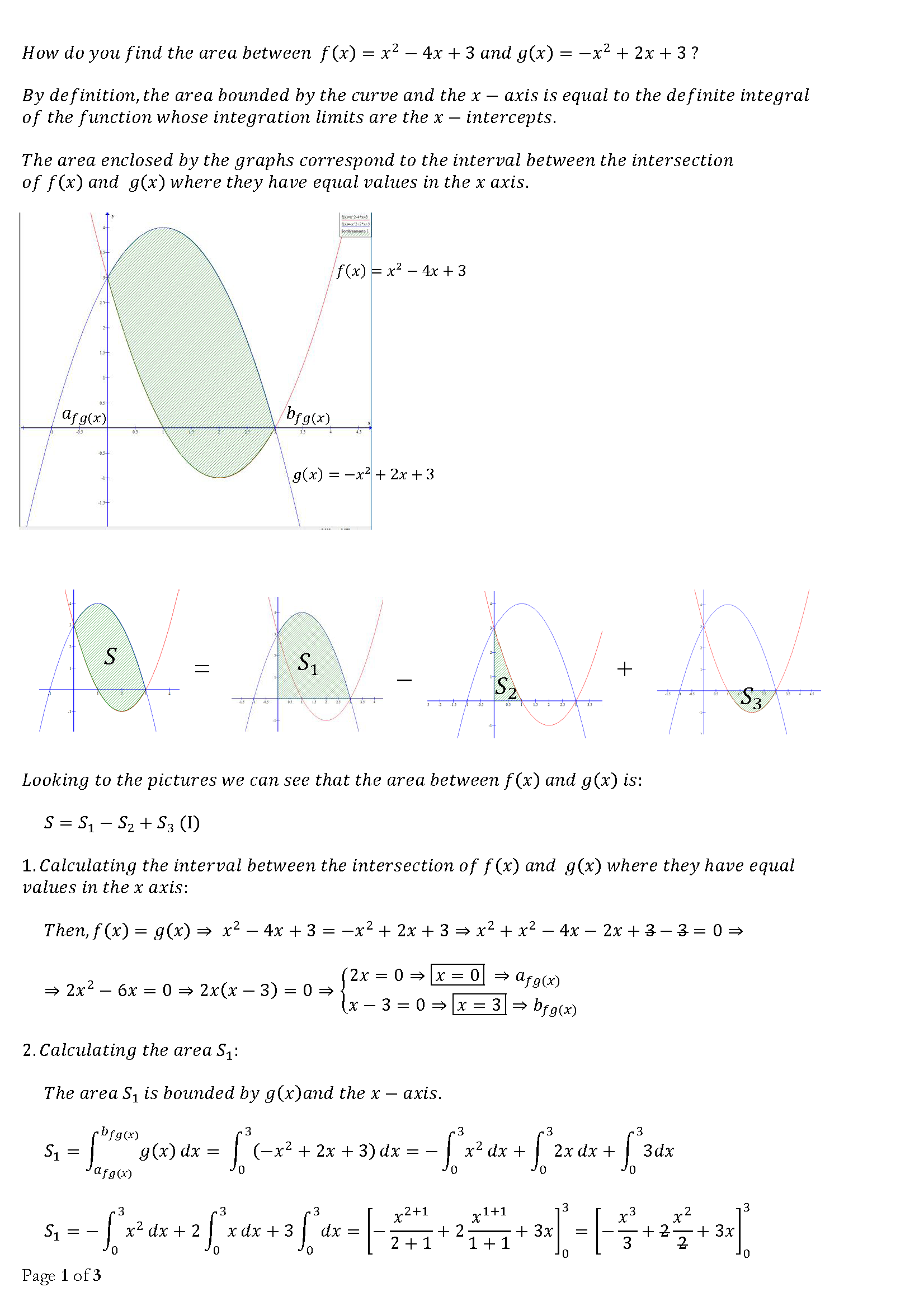



How Do You Find The Area Between F X X 2 4x 3 And G X X 2 2x 3 Socratic



What Is The Area Of The Region Enclosed By The Graphs Of F X X 2x 2 And G X 5x Quora



Http Math Colorado Edu Nita Someexam2practicesol Pdf



Manipulating Graphs



Www Mochidoesmaths Com Composition of functions i Pdf



Math Scene Equations Iii Lesson 3 Quadratic Equations




The Functions F X And G X Are Shown On The Graph F X X2 What Is G X A G X X2 2 B G X Brainly Com




Let F X X 2 And G X 2 X Then The Solution Set Of The Equation Fog X Gof X Is R B 0 C 0 2 D None Of These




Find 1 Gof And 2 Fog Where F X X 2 G X X 2 3x 1 Youtube



0 件のコメント:
コメントを投稿